Normal­vektor

Normalvektoren sind ein grundlegendes Konzept in der Vektorrechnung und spielen eine wichtige Rolle beim MedAT, da man hier sehr leicht Punkte bekommen kann.

Grundlegende Begriffe

Ein Normalvektor ist ein Vektor, der senkrecht (orthogonal) zu einer gegebenen Ebene oder Fläche steht.

Normalvektor in $\mathbb{R}^2$:

In zwei Dimensionen ($\mathbb{R}^2$) steht der Normalvektor senkrecht auf einer Linie. Wenn die Linie durch den Vektor $\vec{a} = \begin{pmatrix} a_1 \\ a_2 \end{pmatrix}$ beschrieben wird, dann ist ein Normalvektor $\vec{n} = \begin{pmatrix} -a_2 \\ a_1 \end{pmatrix}$.

Normalvektor in $\mathbb{R}^3$:
In drei Dimensionen ($\mathbb{R}^3$) berechnet man den Normalvektor zu einer Ebene, die durch zwei Vektoren $\vec{a}$ und $\vec{b}$ aufgespannt wird, mit dem Kreuzprodukt:

$\vec{\mathbf{n}} = \vec{\mathbf{a}} \times \vec{\mathbf{b}}$

$\begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix} \times \begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix}$ $= \begin{pmatrix} a_2 \cdot b_3 \; – \; a_3 \cdot b_2 \\ a_3 \cdot b_1 \; – \; a_1 \cdot b_3 \\ a_1 \cdot b_2 \; – \; a_2 \cdot b_1 \end{pmatrix}$

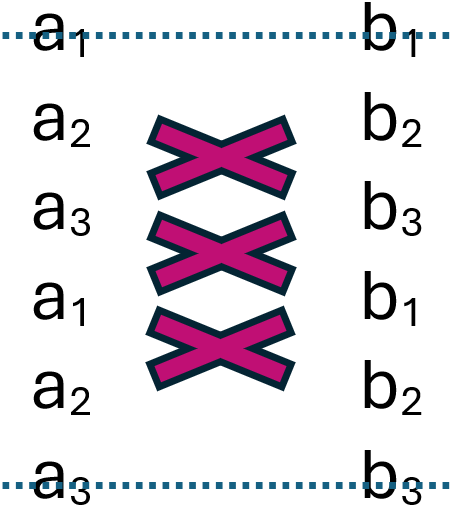
So merkst du dir das Kreuzprodukt leichter:

1. Schreibe die Komponenten der Vektoren je zwei Mal nebeneinander.
2. Streiche die erste und letzte Zeile weg.
3. Kreuze die Produkte der Diagonalen. (Zuerst kommt immer links oben mal rechts unten minus links unten mal rechts oben)

Beispiel (mit Rechenweg)

Beispiel: Normalvektor in $\mathbb{R}^2$: Gegeben sei der Vektor $\vec{a} = \begin{pmatrix} 3 \\ 4 \end{pmatrix}$. Wie lautet der Normalvektor?

Der Normalvektor lautet $\vec{n} = \begin{pmatrix} -4 \\ 3 \end{pmatrix} \quad$ oder $\quad \vec{n} = \begin{pmatrix} 4 \\ -3 \end{pmatrix}$

Beispiel: Normalvektor in $\mathbb{R}^3$: Gegeben seien die Vektoren $\vec{a} = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} \quad$ und $\quad \vec{b} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}$

Der Normalvektor $\vec{n}$ ist: 

$\mathbf{n} = \mathbf{a} \times \mathbf{b}$ $= \begin{pmatrix} 1 \cdot 0 \; – \; 0 \cdot 1 \\ 0 \cdot 0 \; – \; 0 \cdot 1 \\ 1 \cdot 1 \; – \; 0 \cdot 0 \end{pmatrix}$ $= \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}$

Unser Mathe-Insider-Tipp für deinen MedAT

Insider-Tipp von Benjamin (MasterClass-Tutor)

Beim MedAT ist es entscheidend, die Konzepte des Normalvektors und des Kreuzprodukts gut zu verstehen. Für eine gezielte Vorbereitung und weitere nützliche Tipps empfehlen wir dir unsere MasterClass besuchen, bei der wir dieses Thema ausführlich besprechen werden.