Vektor­addition und Vektor­subtraktion

Die Vektoraddition und -subtraktion sind grundlegende Konzepte der Mathematik und für angehende Medizinstudierende, die sich auf den MedAT vorbereiten, unverzichtbar. Sie helfen dabei, komplexe Aufgaben in der Physik und anderen naturwissenschaftlichen Fächern zu lösen und sind zudem schnell verständlich.

Grundlegende Begriffe

Vektoraddition: Bei der Vektoraddition werden die entsprechenden Komponenten zweier Vektoren addiert. Wenn $\vec{a} = \begin{pmatrix} a_1 \\ a_2 \end{pmatrix}$ und $\vec{b} = \begin{pmatrix} b_1 \\ b_2 \end{pmatrix}$ zwei Vektoren sind, dann ist die Summe $\vec{c} = \vec{a} + \vec{b}$ gegeben durch:

$\vec{c}$ = $(a_1 + b_1, a_2 + b_2)$

Vektorsubtraktion: Bei der Vektorsubtraktion werden die entsprechenden Komponenten zweier Vektoren subtrahiert. Wenn $\vec{a} = \begin{pmatrix} a_1 \\ a_2 \end{pmatrix}$ und $\vec{b} = \begin{pmatrix} b_1 \\ b_2 \end{pmatrix}$ zwei Vektoren sind, dann ist die Differenz $\vec{d} = \vec{a} \; – \; \vec{b}$ gegeben durch:

$\vec{d} = \begin{pmatrix} a_1 \; – \; b_1 \\ a_2 \; – \; b_2 \end{pmatrix}$

Beispiel (mit Rechenweg)

Beispiel (rechnerisch): Gegeben seien die Vektoren $\vec{a} = \begin{pmatrix} 3 \\ 4 \end{pmatrix}$ und $\vec{b} = \begin{pmatrix} 1 \\ 2 \end{pmatrix}$.

• Vektoraddition:

$\vec{a} + \vec{b}$ $= \begin{pmatrix} 3 + 1 \\ 4 + 2 \end{pmatrix}$ $= \begin{pmatrix} 4 \\ 6 \end{pmatrix}$

• Vektorsubtraktion:

$\vec{a} – \vec{b}$ $= \begin{pmatrix} 3 \; – \; 1 \\ 4 \; – \; 2 \end{pmatrix}$ $= \begin{pmatrix} 2 \\ 2 \end{pmatrix}$

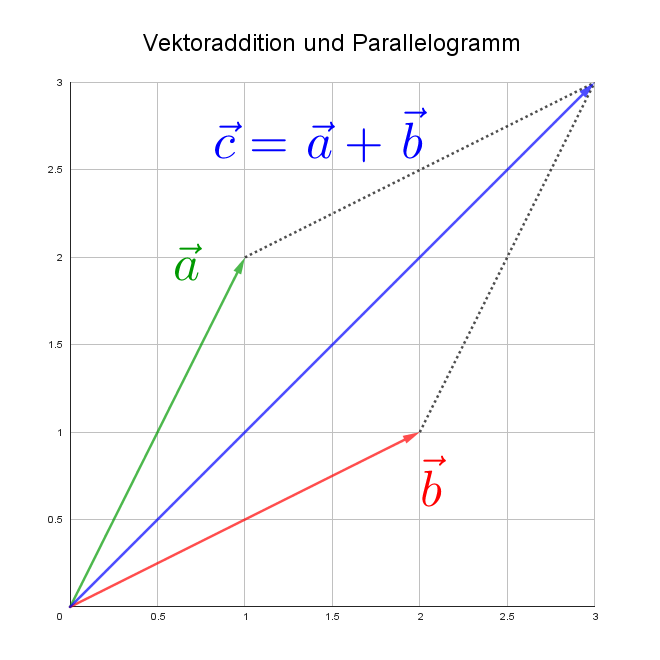
Beispiel (geometrisch):
Geometrisch gesehen entspricht die Addition von Vektoren der Verschiebung eines Vektors um einen anderen. Wenn man die Vektoren $\vec{a}$ und $\vec{b}$ an ihren Ursprungspunkten anlegt, ist die Summe $\vec{c}$ der Vektoren das Diagonalelement des Parallelogramms, das von $\vec{a}$ und $\vec{b}$ gebildet wird. 

Unser Mathe-Insider-Tipp für deinen MedAT

Insider-Tipp von Benjamin (MasterClass-Tutor)

Beim MedAT ist es entscheidend, die Konzepte der Vektoraddition und -subtraktion sowohl rechnerisch als auch geometrisch zu verstehen. Diese Fähigkeiten sind nicht nur für die Lösung mathematischer Aufgaben beim MedAT nützlich, sondern auch später im Studium relevant. Für eine gezielte Vorbereitung und weitere nützliche Tipps empfehlen wir dir unsere E-Learning-Plattform MEDBREAKER ONE….